Heterogeneous Neural Networks¶
Neural networks are probably the most popular machine learning algorithms in recent years. FATE provides a federated Heterogeneous neural network implementation.
This federated heterogeneous neural network framework allows multiple parties to jointly conduct a learning process with partially overlapping user samples but different feature sets, which corresponds to a vertically partitioned virtual data set. An advantage of Hetero NN is that it provides the same level of accuracy as the non privacy-preserving approach while at the same time, reveal no information of each private data provider.
Basic FrameWork¶
The following figure shows the proposed Federated Heterogeneous Neural Network framework.
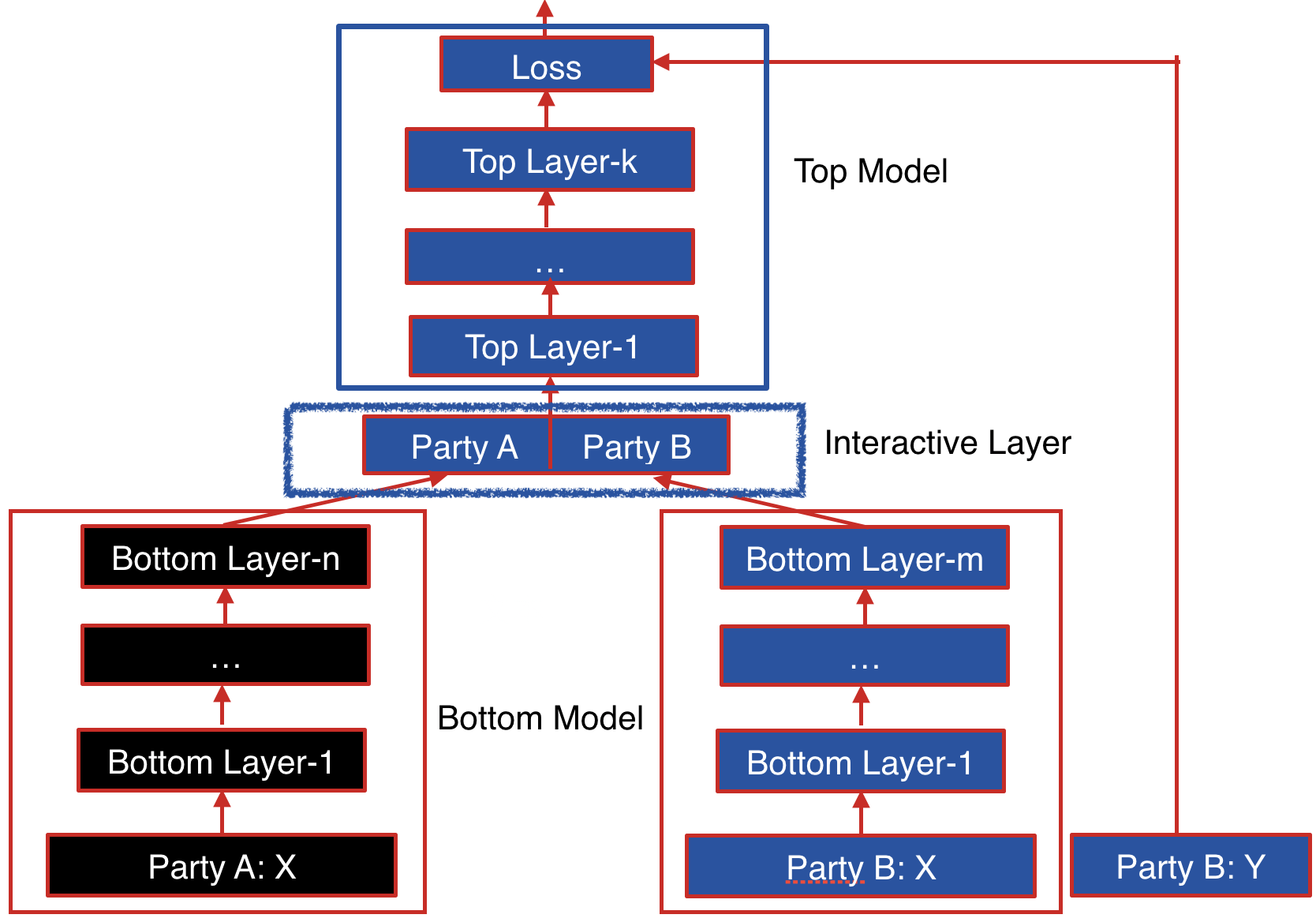
Figure 1 (Framework of Federated Heterogeneous Neural Network)¶
Party B: We define the party B as the data provider who holds both a data matrix and the class label. Since the class label information is indispensable for supervised learning, there must be an party with access to the label y. The party B naturally takes the responsibility as a dominating server in federated learning.
Party A: We define the data provider which has only a data matrix as party A. Party A plays the role of clients in the federated learning setting.
The data samples are aligned under an encryption scheme. By using the privacy-preserving protocol for inter-database intersections, the parties can find their common users or data samples without compromising the non-overlapping parts of the data sets.
Party B and party A each have their own bottom neural network model, which may be different. The parties jointly build the interactive layer, which is a fully connected layer. This layer’s input is the concatenation of the two parties’ bottom model output. In addition, only party B owns the model of interactive layer. Lastly, party B builds the top neural network model and feeds the output of interactive layer to it.
Forward Propagation of Federated Heterogeneous Neural Network¶
Forward Propagation Process consists of three parts.
- Part Ⅰ
Forward Propagation of Bottom Model.
Party A feeds its input features X to its bottom model and gets the forward output of bottom model alpha_A
Party B feeds its input features X to its bottom model and gets the forward output of bottom model alpha_B if active party has input features.
- Part ⅠⅠ
Forward Propagation of Interactive Layer.
Party A uses additive homomorphic encryption to encrypt alpha_A(mark as [alpha _A] ), and sends the encrypted result to party B.
Party B receives the [alpha_A], multiplies it by interactive layer’s party A model weight W_A, get [z_A]. Party B also multiplies its interactive layer’s weight W_B by its own bottom output, getting z_B. Party B generates noise epsilon_B, adds it to [z_A] and sends addition result to party A.
Party A calculates the product of accumulate noise epsilon_acc and bottom input alpha_A (epsilon_acc * alpha_A). Decrypting the received result [z_A + epsilon_B], Party A adds the product to it and sends result to Active party.
Party B subtracts the party A’s sending value by epsilon_B( get z_A + epsilon_acc * alpha_A), and feeds z = z_A + epsilon_acc * alpha_A + z_B(if exists) to activation function.
- Part ⅠⅠⅠ
Forward Propagation of Top Model.
Party B takes the output of activation function’s output of interactive layer g(z) and runs the forward process of top model. The following figure shows the forward propagation of Federated Heterogeneous Neural Network framework.
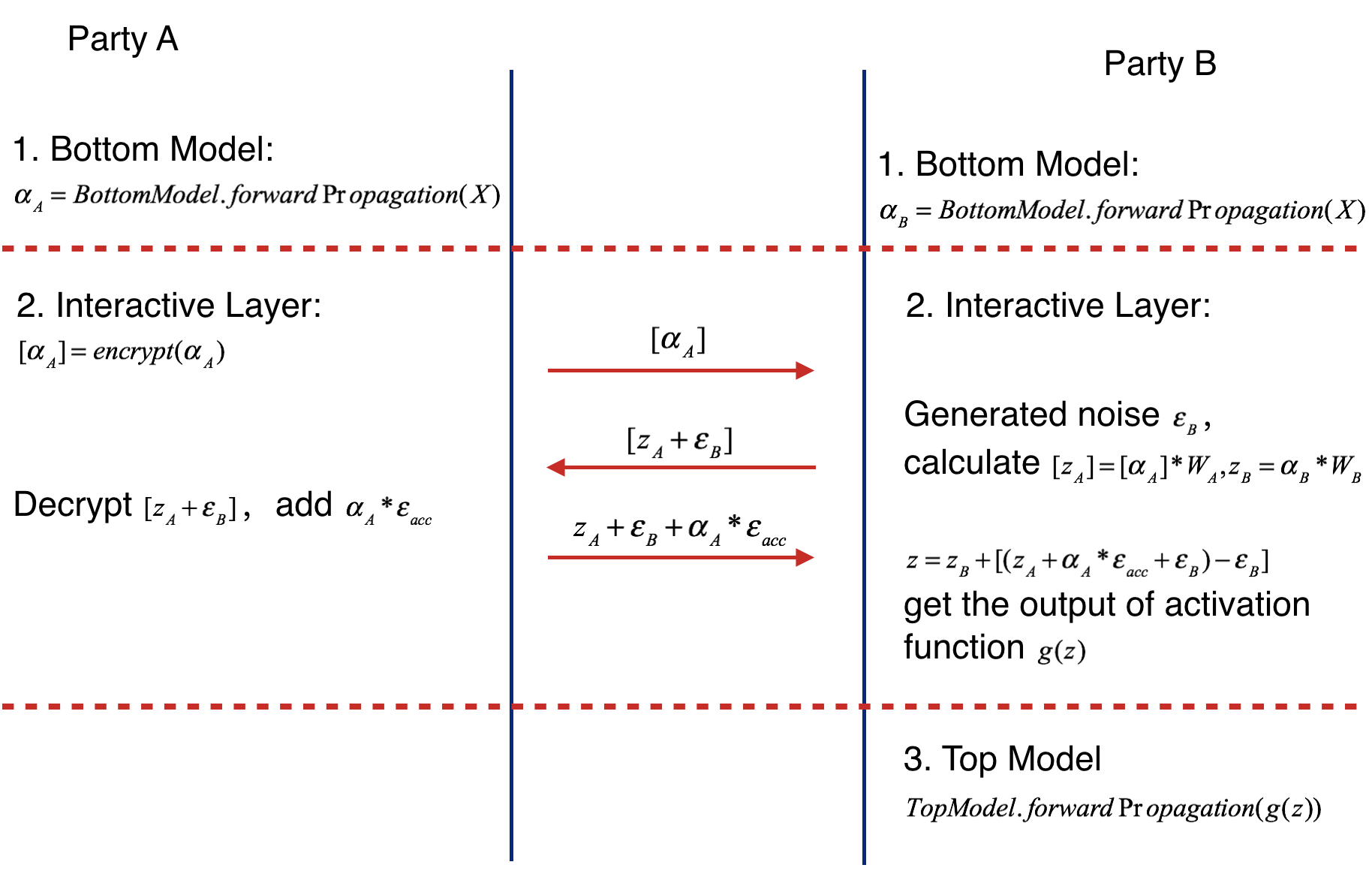
Figure 2 (Forward Propagation of Federated Heterogeneous Neural Network)¶
Backward Propagation of Federated Heterogeneous Neural Network¶
Backward Propagation Process also consists of three parts.
- Part I
Backward Propagation of Top Model.
Party B calculates the error delta of interactive layer output, then updates top model.
- Part II
Backward Propagation of Interactive layer.
Party B calculates the error delta_act of activation function’s output by delta.
Party B propagates delta_bottomB = delta_act * W_B to bottom model, then updates W_B(W_B -= eta * delta_act * alpha_B).
Party B generates noise epsilon_B, calculates [delta_act * (alpha_A + epsilon_B] and sends it to party A.
Party A encrypts epsilon_acc, sends [epsilon_acc] to party B. Then party B decrypts the received value. Party A generates noise epsilon_A, adds epsilon_A / eta to decrypted result(delta_act * alpha_A + epsilon_B + epsilon_A / eta) and add epsilon_A to accumulate noise epsilon_acc(epsilon_acc += epsilon_A). Party A sends the addition result to party B. (delta_act * W_A + epsilon_B + epsilon_A / eta)
Party B receives [epsilon_acc] and delta_act * alpha_A + epsilon_B + epsilon_A / eta. Firstly it sends party A’s bottom model output’ error [delta_act * W_A + acc] to party A. Secondly updates W_A -= eta * (delta_act * W_A + epsilon_B + epsilon_A / eta - epsilon_B) = eta * delta_act * W_A - epsilon_B = W_TRUE - epsilon_acc. Where W_TRUE represents the actually weights.
Party A decrypts [delta_act * (W_A + acc)] and passes delta_act * (W_A + acc) to its bottom model.
- Part III
Backward Propagation of Bottom Model.
Party B and party A updates their bottom model separately. The following figure shows the backward propagation of Federated Heterogeneous Neural Network framework.
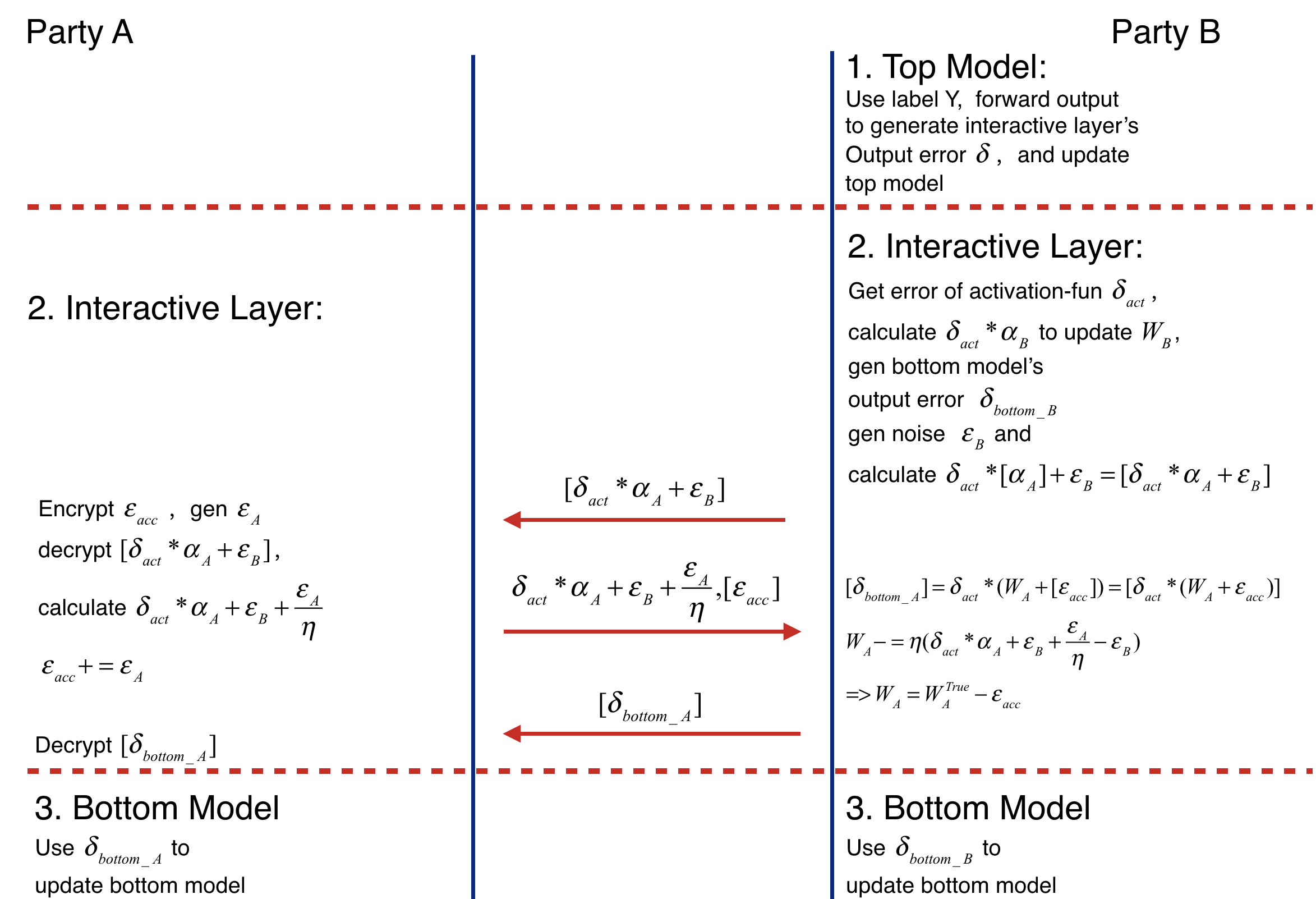
Figure 3 (Backward Propagation of Federated Heterogeneous Neural Network)¶
Param¶
-
class
HeteroNNParam(task_type='classification', config_type='keras', bottom_nn_define=None, top_nn_define=None, interactive_layer_define=None, interactive_layer_lr=0.9, optimizer='SGD', loss=None, epochs=100, batch_size=-1, early_stop='diff', tol=1e-05, encrypt_param=<federatedml.param.encrypt_param.EncryptParam object>, encrypted_mode_calculator_param=<federatedml.param.encrypted_mode_calculation_param.EncryptedModeCalculatorParam object>, predict_param=<federatedml.param.predict_param.PredictParam object>, cv_param=<federatedml.param.cross_validation_param.CrossValidationParam object>, validation_freqs=None, early_stopping_rounds=None, metrics=None, use_first_metric_only=True, selector_param=<federatedml.param.hetero_nn_param.SelectorParam object>, floating_point_precision=23, drop_out_keep_rate=1.0)¶ Parameters used for Hetero Neural Network.
- Parameters
task_type – str, task type of hetero nn model, one of ‘classification’, ‘regression’.
config_type – str, accept “keras” only.
bottom_nn_define – a dict represents the structure of bottom neural network.
interactive_layer_define – a dict represents the structure of interactive layer.
interactive_layer_lr – float, the learning rate of interactive layer.
top_nn_define – a dict represents the structure of top neural network.
optimizer –
optimizer method, accept following types: 1. a string, one of “Adadelta”, “Adagrad”, “Adam”, “Adamax”, “Nadam”, “RMSprop”, “SGD” 2. a dict, with a required key-value pair keyed by “optimizer”,
with optional key-value pairs such as learning rate.
defaults to “SGD”
loss – str, a string to define loss function used
early_stopping_rounds – int, default: None
stop training if one metric doesn’t improve in last early_stopping_round rounds (Will) –
metrics – list, default: None Indicate when executing evaluation during train process, which metrics will be used. If not set, default metrics for specific task type will be used. As for binary classification, default metrics are [‘auc’, ‘ks’], for regression tasks, default metrics are [‘root_mean_squared_error’, ‘mean_absolute_error’], [ACCURACY, PRECISION, RECALL] for multi-classification task
use_first_metric_only – bool, default: False Indicate whether to use the first metric in metrics as the only criterion for early stopping judgement.
epochs – int, the maximum iteration for aggregation in training.
batch_size – int, batch size when updating model. -1 means use all data in a batch. i.e. Not to use mini-batch strategy. defaults to -1.
early_stop –
str, accept ‘diff’ only in this version, default: ‘diff’ Method used to judge converge or not.
diff: Use difference of loss between two iterations to judge whether converge.
validation_freqs –
None or positive integer or container object in python. Do validation in training process or Not. if equals None, will not do validation in train process; if equals positive integer, will validate data every validation_freqs epochs passes; if container object in python, will validate data if epochs belong to this container.
e.g. validation_freqs = [10, 15], will validate data when epoch equals to 10 and 15.
Default: None The default value is None, 1 is suggested. You can set it to a number larger than 1 in order to speed up training by skipping validation rounds. When it is larger than 1, a number which is divisible by “epochs” is recommended, otherwise, you will miss the validation scores of last training epoch.
floating_point_precision –
None or integer, if not None, means use floating_point_precision-bit to speed up calculation, e.g.: convert an x to round(x * 2**floating_point_precision) during Paillier operation, divide
the result by 2**floating_point_precision in the end.
drop_out_keep_rate – float, should betweend 0 and 1, if not equals to 1.0, will enabled drop out
-
class
SelectorParam(method=None, beta=1, selective_size=1024, min_prob=0, random_state=None)¶ Parameters used for Homo Neural Network.
- Parameters
method – None or str, back propagation select method, accept “relative” only, default: None
selective_size – int, deque size to use, store the most recent selective_size historical loss, default: 1024
beta – int, sample whose selective probability >= power(np.random, beta) will be selected
min_prob – Numeric, selective probability is max(min_prob, rank_rate)
Other features¶
Allow party B’s training without features.
Support evaluate training and validate data during training process
Support use early stopping strategy since FATE-v1.4.0
Support selective backpropagation since FATE-v1.6.0
Support low floating-point optimization since FATE-v1.6.0
Support drop out strategy of interactive layer since FATE-v1.6.0
[1] Qiao Zhang, Cong ping strategy since FATE-v1.4.0ang, Hongyping strategy since FATE-v1.4.0 Wu, Chunsheng Xin, Tran V. Phuong. GELU-Net: A Globally Encrypted, Locally Unencrypted Deep Neural Network for Privacy-Preserved Learning. IJCAI 2018: 3933-3939
[2] Yifei Zhang, Hao Zhu. Deep Neural Network for Collaborative Machine Learning with Additively Homomorphic Encryption.IJCAI FL Workshop 2019